Uma cidade tem $2026 \cdot n$ moradores. Qualquer grupo de $2025$ pessoas tem pelo menos um conhecido em comum (que está fora desse grupo de $2025$ pessoas). Mostre que para todo $n$, é possivel escolher um grupo de $n$ moradores tal que cada uma das outras $2025 \cdot n$ pessoas restantes conhece alguêm nesse grupo de $n$ pessoas.
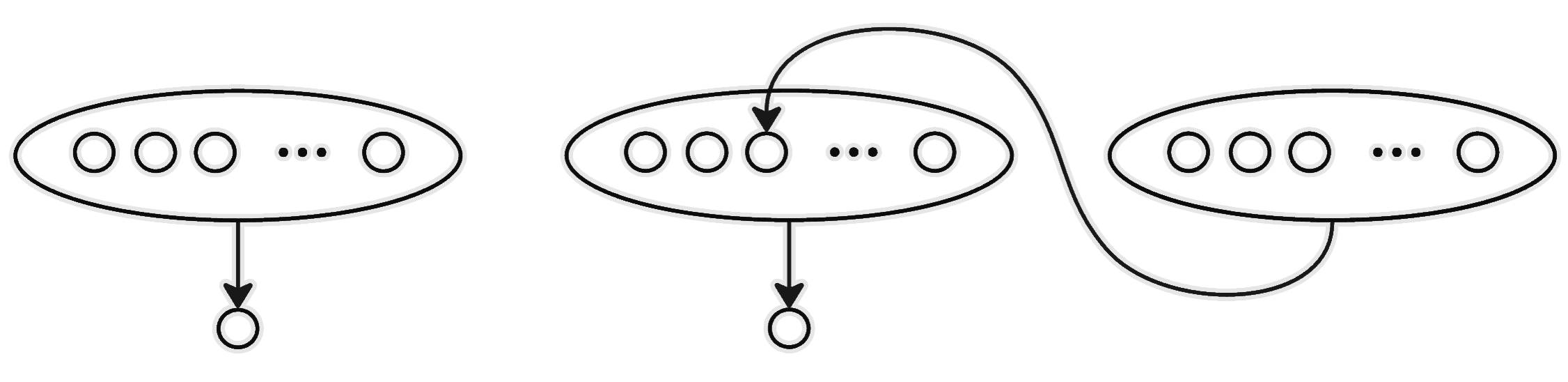
Perceba que o problema não é tão direto quanto simplesmente ir escolhendo o conhecido em comum de uma serie de grupos de $2025$ moradores. Pois pode ser que um dos conhecidos em comum já esteja num grupo de $2025$ que você já selecionou antes, como no exemplo abaixo: