Problema de Maio (2024)

Chegou a edição de Maio/2024 do Problema do Mês! Soluções para o problema podem ser submetidas pelo forms por qualquer aluno de graduação até o dia 31/05. A melhor solução será publicada no Noticiário Eletrônico da SBM! Além disso, a melhor solução de São Carlos receberá uma peça de giz Hagoromo! Elaboramos um ranking com as respostas, portanto soluções bem redigidas e explicadas, com possíveis observações adicionais, serão destacadas. Por outro lado, soluções incompletas também são bem-vindas.

Problema Resolvido
Foto de

Premiado:

Sejam $X, Y, Z$ três pontos não colineares no plano. Mostre que existe um polígono convexo $P$ tal que $P$ pode ser dividido em triângulos de área $1$ e os pontos $X, Y, Z$ são vértices de $P$.

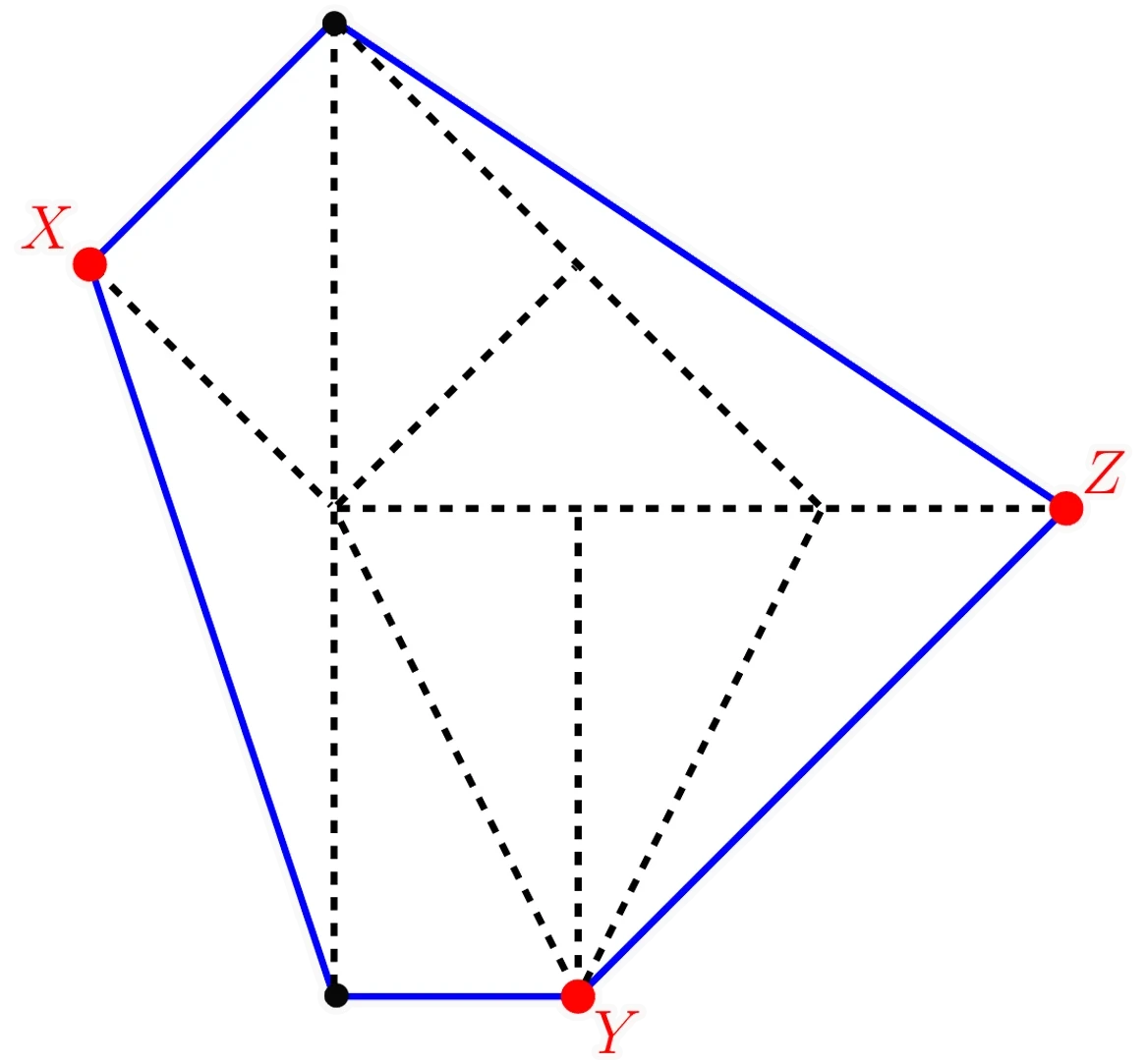
Imagem do Problema

Solution

.